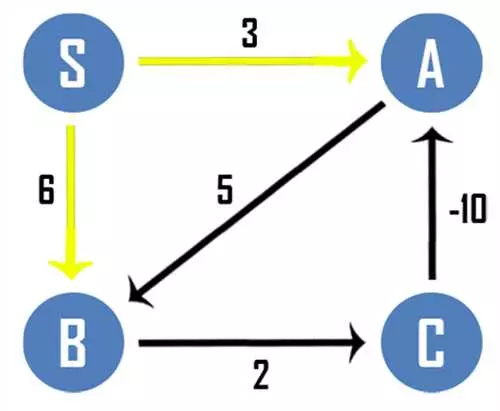
Алгоритмы Беллмана-Форда и Дейкстры – два известных и широко используемых алгоритма в области поиска кратчайшего пути в графах. Оба алгоритма решают эту задачу, но они различаются в своей структуре и подходе к решению.
Алгоритм Дейкстры является алгоритмом с ежекратным выбором вершины, из которой распространяется волна, находящая кратчайший путь. Идея заключается в том, чтобы обрабатывать вершины в порядке увеличения расстояния от начальной вершины, пока не будут обработаны все вершины или не будет найден кратчайший путь до заданной вершины.
Алгоритм Беллмана-Форда, напротив, является алгоритмом с ежекратным обновлением, который рассматривает все ребра графа и выполняет релаксацию. Он повторяет этот процесс V-1 раз, где V – количество вершин в графе. В отличие от алгоритма Дейкстры, алгоритм Беллмана-Форда способен находить кратчайшие пути даже в графах с отрицательными весами ребер.
Преимуществом алгоритма Дейкстры является его эффективность в случае, когда все ребра весовые, и особенно в случае, когда граф является ориентированным ациклическим (DAG). Он имеет временную сложность O((V+E)logV), где V – количество вершин, E – количество ребер графа.
Алгоритм Беллмана-Форда, хотя и является более медленным для обработки чем алгоритм Дейкстры, но он может эффективно обрабатывать графы с отрицательными весами ребер. Поэтому он является предпочтительным выбором в ситуациях, когда существует возможность наличия отрицательных ребер.
- Что такое алгоритм Беллмана-Форда и Дейкстры?
- Алгоритм Дейкстры
- Алгоритм Беллмана-Форда
- Различия между алгоритмом Беллмана-Форда и алгоритмом Дейкстры
- Преимущества алгоритма Беллмана-Форда
- 1. Обработка отрицательных ребер
- 2. Обработка циклов с отрицательным весом
- Преимущества алгоритма Дейкстры
- 1. Эффективность
- 2. Гарантированная корректность
- 3. Простота реализации
- Способы реализации алгоритма Беллмана-Форда
- Способы реализации алгоритма Дейкстры
- 1. Алгоритм Дейкстры с использованием массивов
- 2. Алгоритм Дейкстры с использованием кучи
- Зависимость времени выполнения от размера графа
- Особенности работы алгоритма Беллмана-Форда на отрицательных графах
- Принцип работы
- Отрицательные циклы
- Преимущества алгоритма Беллмана-Форда
- Особенности работы алгоритма Дейкстры на отрицательных графах
- Сферы применения алгоритма Беллмана-Форда
- Транспорт и логистика
- Сети связи и телекоммуникации
- Торговля и финансы
- Сферы применения алгоритма Дейкстры
- Как выбрать правильный алгоритм для конкретной задачи?
- 💡 Видео
Видео:АЛГОРИТМ БЕЛЛМАНА-ФОРДА — ИДЕЯ И РЕАЛИЗАЦИЯ (ЧАСТЬ 1)Скачать

Что такое алгоритм Беллмана-Форда и Дейкстры?
Алгоритм Дейкстры
Алгоритм Дейкстры работает только для ориентированных графов с неотрицательными весами ребер. Он начинает с определения стартовой вершины и присваивания ей расстояния 0, а остальным вершинам — бесконечность. Затем алгоритм итеративно выбирает вершину с наименьшим расстоянием, обновляет расстояние до соседних вершин и повторяет этот процесс до тех пор, пока не будут обработаны все вершины. Однако, алгоритм Дейкстры не может обрабатывать ребра с отрицательными весами, так как в этом случае может возникнуть бесконечный цикл.
Алгоритм Беллмана-Форда
Алгоритм Беллмана-Форда является более общим и может обрабатывать графы с ребрами любых весов, в том числе и с отрицательными. Он начинает с присваивания стартовой вершине расстояния 0, а остальным — бесконечность. Затем алгоритм выполняет следующий шаг: для каждого ребра графа проверяет, можно ли улучшить минимальное расстояние до текущей вершины, используя данное ребро. Этот шаг выполняется V-1 раз, где V — количество вершин в графе.
Одно из главных преимуществ алгоритма Беллмана-Форда — его способность обрабатывать ребра с отрицательными весами. Алгоритм может обнаружить и решить проблемы отрицательных циклов. Кроме того, алгоритм может использоваться для поиска кратчайшего пути за один проход, в отличие от алгоритма Дейкстры, который требует нескольких проходов для каждой вершины.
Видео:BP2-3-3-08 Алгоритм Форда-БеллманаСкачать

Различия между алгоритмом Беллмана-Форда и алгоритмом Дейкстры
Однако, несмотря на то, что оба алгоритма находят кратчайшие пути в графах, они имеют ряд существенных различий. Главное различие между ними — в том, что алгоритм Беллмана-Форда может работать с графами, содержащими отрицательные ребра, в то время как алгоритм Дейкстры не способен обработать графы с отрицательными ребрами.
Еще одно отличие заключается в том, что алгоритм Дейкстры работает только с графами без ребер отрицательной длины, в то время как алгоритм Беллмана-Форда может обрабатывать такие графы.
Дейкстров алгоритм работает по принципу жадного выбора, то есть на каждом шаге он выбирает вершину с наименьшим весом, добавляет ее в дерево кратчайших путей и обновляет расстояния до остальных вершин. Алгоритм Беллмана-Форда, в свою очередь, рассматривает все возможные ребра и оптимизирует длину пути для каждой вершины, обновляя расстояния на каждой итерации.
Еще одно отличие алгоритма Беллмана-Форда от алгоритма Дейкстры заключается в том, что Беллмана-Форда может обнаружить наличие отрицательных циклов в графе. Это означает, что если граф содержит цикл отрицательного веса, алгоритм Беллмана-Форда сообщит об этом, в то время как алгоритм Дейкстры может зациклиться и не найти кратчайший путь.
Таким образом, хотя оба алгоритма являются эффективными инструментами для нахождения кратчайших путей в графах, алгоритм Беллмана-Форда более универсален, так как может работать с графами, содержащими отрицательные ребра и обнаруживать отрицательные циклы. В то же время, алгоритм Дейкстры более эффективен для работы с графами без ребер отрицательной длины и может быть лучшим вариантом в таких случаях.
Видео:Алгоритм Форда-Беллмана и SPFAСкачать

Преимущества алгоритма Беллмана-Форда
1. Обработка отрицательных ребер
Одним из основных преимуществ алгоритма Беллмана-Форда является его способность работать с графами, содержащими отрицательные ребра. В отличие от алгоритма Дейкстры, который не может быть применен к таким случаям, алгоритм Беллмана-Форда позволяет находить кратчайший путь, даже если в графе есть отрицательные ребра. Это делает его более универсальным и применимым в реальных задачах.
2. Обработка циклов с отрицательным весом
Алгоритм Беллмана-Форда также может обрабатывать графы с циклами, содержащими отрицательный вес. В таких случаях алгоритм может обнаружить наличие цикла с отрицательным весом и указать на то, что в графе нет кратчайшего пути. Это полезно, когда необходимо определить, существуют ли такие циклы и как они влияют на решение задачи.
Кроме того, алгоритм Беллмана-Форда позволяет определять наличие отрицательного цикла в графе. Это позволяет решить задачу обнаружения отрицательного цикла и использовать результаты для оптимизации процесса поиска кратчайших путей.
В целом, алгоритм Беллмана-Форда предоставляет больше гибкости и возможностей, чем алгоритм Дейкстры, при работе с взвешенными ориентированными графами. Его способность обрабатывать отрицательные ребра и циклы с отрицательным весом делает его особенно полезным в решении реальных задач, где такие ситуации могут возникать.
Видео:Алгоритм Беллмана-Форда | Bellman-Ford algorithmСкачать

Преимущества алгоритма Дейкстры
1. Эффективность
Алгоритм Дейкстры работает эффективно для графов с небольшим количеством вершин и ребер. В худшем случае, сложность алгоритма составляет O(|V|^2), где |V| — количество вершин в графе. Однако, при использовании приоритетной очереди, сложность может быть улучшена до O((|V| + |E|) log |V|), где |E| — количество ребер в графе. Таким образом, алгоритм Дейкстры работает значительно быстрее алгоритма Беллмана-Форда для больших графов.
2. Гарантированная корректность
Алгоритм Дейкстры гарантированно находит кратчайшие пути от заданной вершины до всех остальных вершин в графе. Это свойство очень полезно, если требуется найти кратчайшие пути от одной вершины до всех остальных взвешенного графа. В отличие от алгоритма Беллмана-Форда, который может быть использован для поиска отрицательных циклов, алгоритм Дейкстры работает только с положительными весами ребер.
3. Простота реализации
Алгоритм Дейкстры относительно прост в реализации. Он не требует сложной структуры данных и сравнительно небольшого количества операций. Это делает его удобным для использования в практических задачах, где требуется быстро найти кратчайшие пути в графе с положительными весами ребер.
| Алгоритм Дейкстры | Алгоритм Беллмана-Форда |
|---|---|
| Работает только с положительными весами ребер | Может работать с отрицательными весами ребер |
| Сложность O((|V| + |E|) log |V|) | Сложность O(|V| * |E|) |
| Кратчайшие пути гарантированно найдены | Может работать с циклами отрицательной стоимости |
Видео:Алгоритм Дейкстры. САМОЕ ПОНЯТНОЕ ОБЪЯСНЕНИЕСкачать
Способы реализации алгоритма Беллмана-Форда
Алгоритм Беллмана-Форда предназначен для нахождения кратчайшего пути в направленном взвешенном графе с возможностью существования отрицательных ребер. Рассмотрим несколько способов его реализации:
- Итерационный подход:
- Задаем начальное расстояние от исходной вершины до всех остальных вершин равным бесконечности, а до самой себя – равным нулю.
- Выполняем n-1 итераций, где n – количество вершин в графе.
- На каждой итерации обновляем расстояния до вершин с использованием формулы: d[v] = min(d[v], d[u] + w(u, v)), где d[v] – расстояние до вершины v, d[u] – расстояние до вершины u, w(u, v) – вес ребра из u в v.
- На каждой итерации проверяем, не обновилось ли расстояние до вершины, и в случае обновления, прекращаем дальнейшую обработку.
- В конечном итоге получаем кратчайшие пути до всех вершин графа.
- Модификация алгоритма с ранней остановкой:
- При выполнении итераций добавляем переменную, отслеживающую флаг обновления расстояний.
- Если на данной итерации ни одно расстояние до вершины не обновилось, устанавливаем флаг в false и прекращаем обработку графа.
- Этот подход позволяет сократить работу алгоритма в случае, когда дальнейшие обновления расстояний не влияют на результат.
- Оптимизация с использованием очереди:
- Вместо обработки всех ребер на каждой итерации, использовать очередь, содержащую вершины, расстояния до которых были обновлены на текущей и предыдущей итерациях.
- При обработке вершины из очереди, обновлять расстояния до смежных вершин.
- При обновлении расстояния до вершины, добавлять ее в очередь.
- Этот подход позволяет уменьшить количество обрабатываемых ребер на каждой итерации, что ускоряет работу алгоритма.
Основные преимущества алгоритма Беллмана-Форда включают возможность работы с графами, содержащими отрицательные ребра и циклы отрицательного веса, а также способность найти кратчайший путь из одной вершины во все остальные. Выбор конкретного способа реализации зависит от требуемой производительности и особенностей графа.
Видео:ДС Алгоритм Беллмана-ФордаСкачать

Способы реализации алгоритма Дейкстры
1. Алгоритм Дейкстры с использованием массивов
Наиболее простой и понятный способ реализации алгоритма Дейкстры – использование массивов. В этом случае каждая вершина графа представляется в виде индекса массива, а значение в ячейке массива соответствует кратчайшей известной длине пути к данной вершине.
Алгоритм начинает с инициализации массива значений бесконечностью для всех вершин, кроме стартовой вершины, для которой устанавливается значение 0. Затем алгоритм проходит по всем смежным вершинам и обновляет их значения в случае нахождения более короткого пути. Алгоритм продолжается до тех пор, пока все вершины не будут обработаны.
2. Алгоритм Дейкстры с использованием кучи
Другим способом реализации алгоритма Дейкстры является использование кучи (или пирамиды). Куча представляет собой структуру данных, в которой каждый элемент имеет значение приоритета. Основная идея этого способа заключается в том, что на каждом шаге алгоритма выбирается вершина с наименьшим значением в куче, что позволяет обрабатывать более эффективно и ускоряет время выполнения.
Алгоритм начинается с инициализации кучи и добавления в нее стартовой вершины с приоритетом 0. Затем на каждом шаге алгоритма выбирается вершина с наименьшим значением, и их смежные вершины обновляются, если находится более короткий путь. После обновления, вершина добавляется в кучу с обновленным значением. Алгоритм продолжается до тех пор, пока все вершины не будут обработаны.
При правильной реализации алгоритм Дейкстры может быть выполнен за время O((V + E) * log(V)), где V – количество вершин, а E – количество ребер.
Видео:Алгоритмы (базовый поток) 10. Алгоритм Дейкстры, Форда-БеллманаСкачать

Зависимость времени выполнения от размера графа
Одним из главных отличий между алгоритмами Беллмана-Форда и Дейкстры является их асимптотическая временная сложность. Алгоритм Дейкстры имеет временную сложность O((V + E)logV), где V — количество вершин, E — количество ребер в графе. В то время как алгоритм Беллмана-Форда имеет временную сложность O(VE), что делает его менее эффективным для больших графов, содержащих много ребер.
Зависимость времени выполнения алгоритма от размера графа особенно заметна при работе с крупными графами. В случае алгоритма Дейкстры, его временная сложность зависит от количества вершин и ребер в графе. При увеличении количества вершин и ребер, время выполнения алгоритма увеличивается. Однако, благодаря использованию кучи (heap) для организации приоритетной очереди, алгоритм Дейкстры все равно остается эффективным для большинства задач.
В случае алгоритма Беллмана-Форда, его временная сложность зависит линейно от количества вершин и ребер. Это означает, что с увеличением размера графа, время выполнения алгоритма также увеличивается линейно. Алгоритм Беллмана-Форда имеет преимущество в том, что он может работать с графами, содержащими отрицательные ребра или циклы отрицательного веса. Однако, для графов большого размера алгоритм может стать слишком медленным.
Таким образом, выбор алгоритма поиска кратчайшего пути зависит от размера графа и особенностей самой задачи. Алгоритм Дейкстры является эффективным для большинства задач с малым или средним размером графа. Алгоритм Беллмана-Форда, в свою очередь, подходит для решения задач с графами большого размера и способен обрабатывать графы с отрицательными ребрами или циклами отрицательного веса.
Видео:Алгоритм ДейкстрыСкачать

Особенности работы алгоритма Беллмана-Форда на отрицательных графах
Алгоритм Беллмана-Форда используется для нахождения кратчайшего пути в графе с отрицательными весами ребер. Он отличается от алгоритма Дейкстры своей способностью работать на графах с отрицательными циклами.
Принцип работы
Алгоритм Беллмана-Форда использует итеративный подход, основанный на повторении проходов по всем ребрам графа. На каждом шаге алгоритма обновляются оценки расстояний до всех вершин, и в процессе выполнения алгоритма своего рода релаксации происходят до тех пор, пока все вершины не получат окончательные значения.
Отрицательные циклы
Одной из особенностей работы алгоритма Беллмана-Форда на отрицательных графах является возможность обнаружения и обработки отрицательных циклов. Это значит, что алгоритм может выявить ситуацию, когда сумма весов ребер в замкнутом пути отрицательна, и отказаться от поиска кратчайшего пути, чтобы избежать зацикливания и бесконечного уменьшения длины пути.
Однако, наличие отрицательных циклов может привести к тому, что алгоритм Беллмана-Форда не сможет найти решение, так как не существует кратчайшего пути в графе с отрицательным циклом. В этом случае алгоритм будет сообщать о наличии отрицательного цикла и не будет возвращать результат.
Преимущества алгоритма Беллмана-Форда
- Способность работать с графами, содержащими отрицательные ребра и отрицательные циклы.
- Возможность использования алгоритма для определения наличия отрицательных циклов в графе.
- Простота реализации и понятность алгоритма.
Алгоритм Беллмана-Форда является полезным инструментом при работе с графами, содержащими отрицательные веса ребер. Он позволяет находить кратчайшие пути и выявлять отрицательные циклы, что может быть важным в контексте задач планирования маршрутов, логистики, вычислительной геометрии и других областей, где возникают отрицательные веса ребер.
Видео:Зимова школа 2024 - Разбор задач - Алгоритмы Дейкстры и Беллмана-ФордаСкачать
Особенности работы алгоритма Дейкстры на отрицательных графах
При работе с отрицательными графами алгоритм Дейкстры может привести к некорректным результатам. Это связано с тем, что алгоритм Дейкстры предполагает, что все веса ребер в графе являются положительными. В случае присутствия отрицательных весов, алгоритм может выбрать неправильный кратчайший путь или зациклиться.
Тем не менее, существуют модификации алгоритма Дейкстры, которые позволяют работать с графами, в которых присутствуют отрицательные веса ребер. Одним из таких модифицированных алгоритмов является алгоритм Дейкстры с отслеживанием отрицательных циклов.
Алгоритм Дейкстры с отслеживанием отрицательных циклов работает следующим образом:
- Инициализация.
- Установка начальной вершины.
- Пометка начальной вершины как посещенной и установка ее расстояния до нее же равным 0.
- Цикл.
- Выбор вершины, для которой еще не вычислено окончательное кратчайшее расстояние.
- Расчет расстояний до соседних вершин выбранной вершины.
- Если кратчайший путь до соседней вершины через выбранную вершину и меньше текущего кратчайшего пути до соседней вершины, то обновляем кратчайший путь до соседней вершины.
- Пометка выбранной вершины как посещенной.
- Повторение шагов 5-8, пока не будут посещены все вершины или не будут обработаны все ребра.
- Проверка наличия отрицательных циклов.
Алгоритм Дейкстры с отслеживанием отрицательных циклов обнаруживает наличие отрицательных циклов, что позволяет избежать некорректных результатов. Если в графе присутствует отрицательный цикл, то алгоритм будет работать бесконечно, так как с каждой итерацией путь до вершины будет уменьшаться.
Однако, стоит отметить, что алгоритм Дейкстры с отслеживанием отрицательных циклов все равно не может обрабатывать графы с отрицательными циклами. В таких случаях необходимо использовать алгоритм Беллмана-Форда или другие подходящие алгоритмы.
Видео:Задача о максимальном потоке в сети, часть 1Скачать

Сферы применения алгоритма Беллмана-Форда
Транспорт и логистика
Алгоритм Беллмана-Форда находит применение в области транспорта и логистики. Он может использоваться для оптимизации маршрутов доставки грузов, учитывая различные факторы, такие как пропускные способности дорог и временные задержки. Алгоритм позволяет найти кратчайший путь с минимальными затратами, учитывая сложности и ограничения, такие как возможность пересечения границ или наличие дорожных сборов.
Сети связи и телекоммуникации
В сетях связи и телекоммуникациях алгоритм Беллмана-Форда может использоваться для выбора оптимального пути передачи данных. Он учитывает стоимость передачи данных через каждое соединение и находит наименьшее время передачи от исходной точки до сколь угодно долгой цели. Это позволяет оптимизировать сетевые ресурсы и гарантирует минимальные задержки в передаче данных.
Торговля и финансы
В финансовой сфере алгоритм Беллмана-Форда может использоваться для поиска арбитражных возможностей на рынке обмена валюты или финансовых инструментов. Он позволяет определить последовательность операций с минимальными затратами, учитывая различные валютные курсы и комиссии. Алгоритм также может быть использован для прогнозирования будущих рыночных трендов на основе исторических данных и весов ребер графа.
- Алгоритм Беллмана-Форда является основным инструментом для решения задач кратчайшего пути в графе с отрицательными весами.
- Он применим в области транспорта и логистики, сетей связи и телекоммуникаций, торговли и финансов.
- Алгоритм позволяет оптимизировать расходы, выбирая наиболее дешевые и быстрые пути передвижения или передачи данных.
- Он также может использоваться для прогнозирования будущих трендов и арбитражных возможностей на рынке.
Видео:Алгоритм Дейкстры или как навигатор определяет оптимальный маршрутСкачать

Сферы применения алгоритма Дейкстры
Алгоритм Дейкстры нашел широкое применение в различных областях, включая:
1. Транспорт и логистика:
Алгоритм Дейкстры может помочь оптимально построить пути для грузовых машин, общественного транспорта и авиаперевозок. Он может быть использован для оптимизации маршрутов доставки груза, позволяя минимизировать затраты на топливо и время.
2. Сетевое планирование:
Алгоритм Дейкстры применяется для определения оптимальных путей в компьютерных сетях, таких как Интернет, сети связи и телекоммуникационные сети. Он позволяет оптимизировать маршрутизацию трафика, учитывая пропускную способность и задержки в сети.
3. Визуализация данных:
Алгоритм Дейкстры может быть использован для визуализации данных, основанных на графах. Он позволяет определить наиболее значимые связи между узлами графа и найти пути с наименьшими затратами или максимальной пропускной способностью.
4. Планирование задач:
Алгоритм Дейкстры может быть применен для решения задач планирования, таких как оптимальное распределение ресурсов или составление графиков работ. Он помогает найти наиболее эффективные пути выполнения работ и оптимизировать распределение времени и ресурсов.
Алгоритм Дейкстры является мощным инструментом для решения задач о кратчайшем пути, он обладает высокой производительностью и может быть адаптирован для различных сфер применения. Внимательное и грамотное использование этого алгоритма может значительно улучшить эффективность и оптимизировать многие процессы.
Видео:Графы: Алгоритм Форда БеллманаСкачать

Как выбрать правильный алгоритм для конкретной задачи?
При выборе алгоритма для решения конкретной задачи, важно учитывать ряд факторов, которые могут влиять на эффективность и точность решения. Ниже представлены некоторые рекомендации, которые помогут вам сделать правильный выбор.
- Определите тип задачи: перед вами может стоять задача нахождения кратчайшего пути, задача поиска минимального остовного дерева или задача поиска экстремальных значений.
- Учтите особенности графа: алгоритмы Беллмана-Форда и Дейкстры применяются для графов с положительными и отрицательными весами ребер, однако Беллман-Форд может обрабатывать графы с ребрами отрицательного цикла.
- Оцените сложность времени выполнения алгоритмов: в зависимости от размера графа и требуемой точности решения, необходимо выбрать алгоритм с наименьшей сложностью.
- Учитывайте возможность наличия отрицательных циклов: если задача может содержать отрицательные циклы, то алгоритм Беллмана-Форда будет предпочтительней, так как Дейкстры не способен обработать такие графы.
- Анализируйте ограничения на память: если у вас ограниченный объем памяти, то следует выбирать алгоритм, который потребляет меньше ресурсов.
Выбор правильного алгоритма может существенно повлиять на результат решения задачи. При правильном подборе алгоритма можно добиться оптимальной производительности и точности решения, что является важным фактором во многих областях, включая транспорт, логистику и информационные технологии.
💡 Видео
Граф(4 урок)( Алгоритм Белмана-Форда)Скачать

4.6 Алгоритм Форда-БеллманаСкачать

Алгоритмы и структуры данных 9. Продолжение кратчайших путей. А*, Флойд, Форд-БеллманСкачать

Принцип оптимальности БеллманаСкачать

Программирование основных алгоритмов 3. Алгоритмы Дейкстры, Форда-Беллмана, Флойда-УоршеллаСкачать

АиСД S03E07. Алгоритмы Форда-Беллмана и Флойда-УоршеллаСкачать

Алгоритмы и структуры данных (продвинутый поток) 7. BFS, Алгоритм Дейкстры, Форда-БеллманаСкачать

Алгоритмы и структуры данных 6. BFS, алгоритмы Дейкстры и Форда-БеллманаСкачать